Text is all around us; essays, articles, legal documents, text messages, and news headlines are consistently present in our daily lives. This abundance of text provides ample opportunities to analyze unstructured data.
Imagine you are playing a game where someone hands you a index card with the misspelled name of a popular musician. In addition, you have a book containing correctly spelled names of popular musicians. The goal is for you to return the correct spelling of the misspelled name.
In this example, suppose someone hands you a card with “Billie Jole” written on it. You quickly open the book of musicians, find names beginning with the letter B, and find the name “Billy Joel.”
As a human, this was easy for you to complete, but what if you wanted to automate this task? This can be done using Fuzzy Logic, or more specifically, the Levenshtein distance.
The Levenshtein distance considers two pieces of text and determines the minimum number of changes required to convert one string into another. You can utilize this logic to find the closest match to any given piece of text.
I am going to focus on implementing the mechanics of finding a Levenshtein distance in Python rather than the math that makes it possible. There are many resources on YouTube which explain how the Levenshtein distance is calculated.
First, import numpy and define a function. I called the function lv as shorthand for Levenshtein distance. Our function requires two input strings which are used to create a 2D matrix that is one greater than the length of each string.
def ld(s1, s2):
rows = len(s1)+1
cols = len(s2)+1
dist = np.zeros([rows,cols])If you were to use the strings “pear” and “peach” in this instance, the function should create a 5 by 6 matrix filled with zeros.

Next, the first row and column need to count up from zero. Using for loops, we can iterate over the selected values. Our Python function now creates the following matrix.
def ld(s1, s2):
rows = len(s1)+1
cols = len(s2)+1
dist = np.zeros([rows,cols])
for i in range(1, rows):
dist[i][0] = i
for i in range(1, cols):
dist[0][i] = i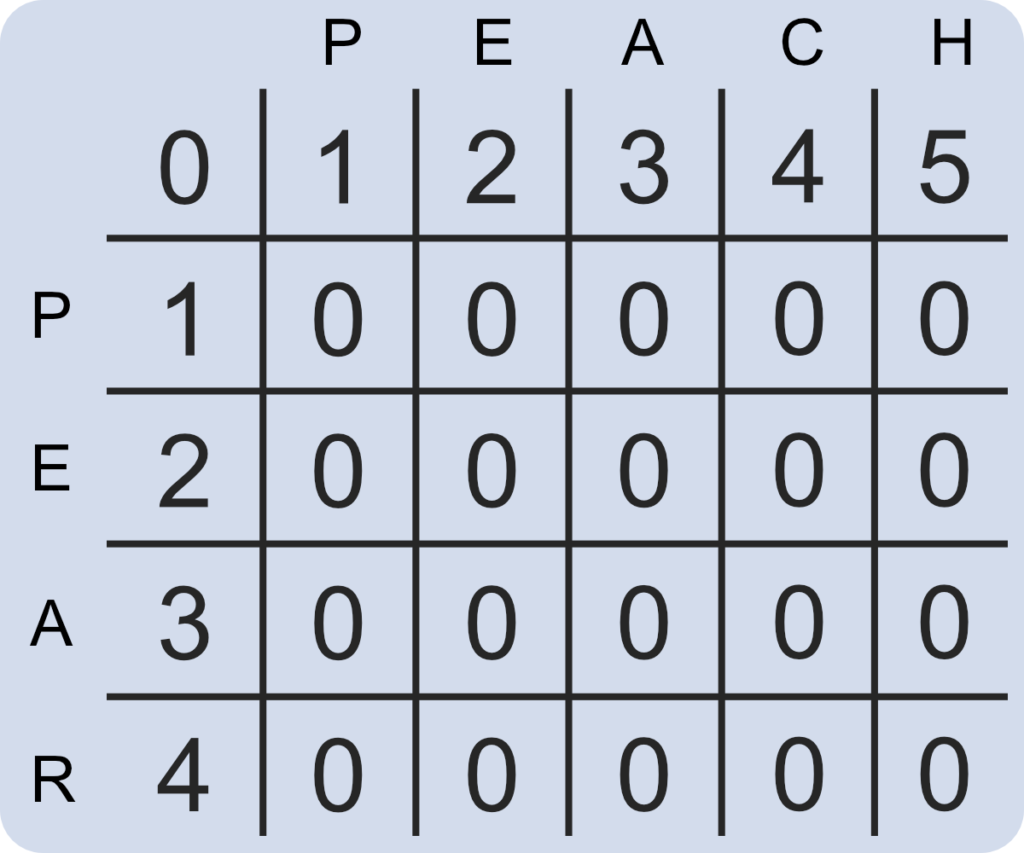
Finally, we need to iterate over every column and row combination. By doing this, we can find the minimum value of the cells directly above, to the left, and above to the left of each cell. After the minimum is found, our Python script adds one to this value to the location in question.
def ld(s1, s2):
rows = len(s1)+1
cols = len(s2)+1
dist = np.zeros([rows,cols])
for i in range(1, rows):
dist[i][0] = i
for i in range(1, cols):
dist[0][i] = i
for col in range(1, cols):
for row in range(1, rows):
if s1[row-1] == s2[col-1]:
cost = 0
else:
cost = 1
dist[row][col] = min(dist[row-1][col] + 1,
dist[row][col-1] + 1,
dist[row-1][col-1] + cost)
return dist[-1][-1]
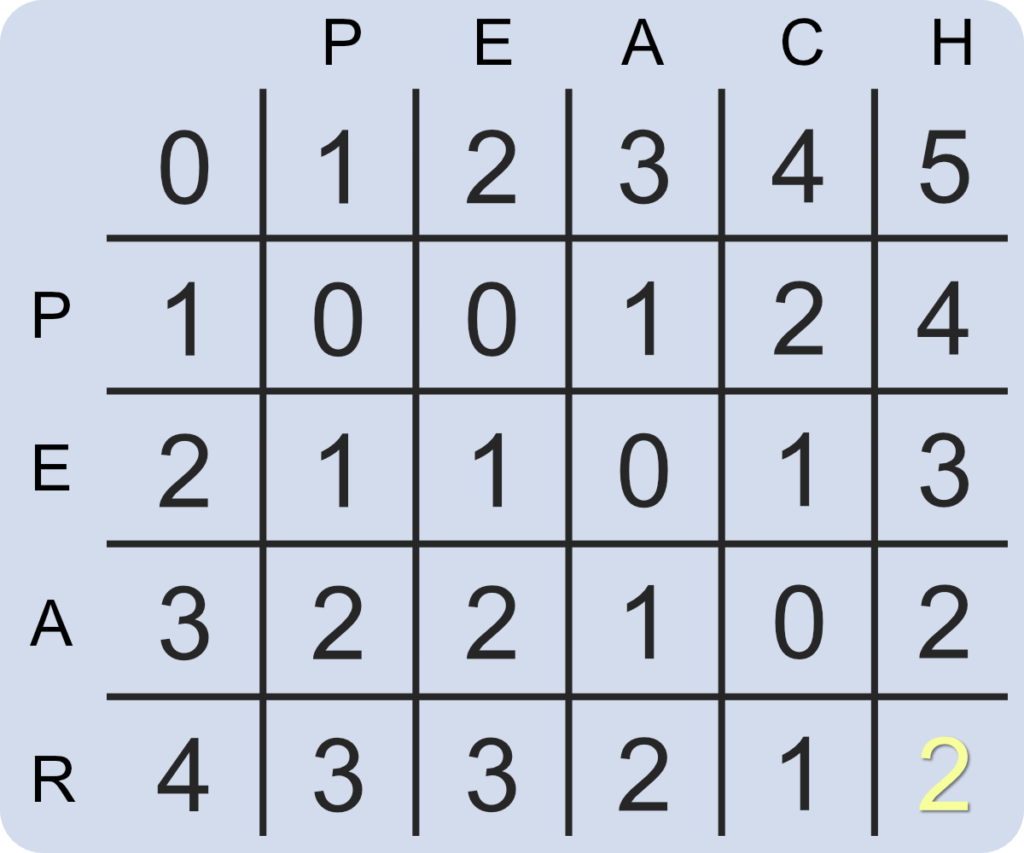
Our matrix should now look like the following with the far bottom right cell representing the number of changes required to convert one string into another. In this instance, it requires 2 changes to convert “peach” into “pear”; deleting the letter “c” in “peach” and replacing the letter “h” with the letter “r”.
What is so great about this function is that it is adaptable and will accept a string of any length to compute the number of changes required. While the mechanics behind this function are relatively simple, its use cases are vast.
