Playing bingo is not all that interesting, however, simulating bingo is much more fun! Today I wrote some Python which performs stochastic bingo simulations across a number of rounds and number of players.
Specifically, I simulated a bingo game with 20 rounds for n players. This allows us to determine a few things. But first, a little terminology:
- Player: An individual bingo board which lasts for only one round
- Turn: A random number which is drawn and applied to all current players
- Round: Resets all bingo boards for n players
- Game: A number of bingo rounds
I wanted to know the average number of turns within a round of bingo. We would expect the number of turns per round to fall for larger numbers of players because there is greater opportunity for someone to win.
Additionally, I also wanted to know the probability of winning bingo at least once for n players. Fortunately, this is simple to compute with math. Lets assume there are 100 players, 20 rounds, and an equal chance to win each round with replacement.
We can compute the probability of not winning each round. With 100 players this is 0.99. If we take this to the power of 20, representing the number of rounds, we get the probability of not winning. Thus the probability of winning is 1 minus this value:
![]()
Now lets validate this with code!
import numpy as np
from random import sample, choice
class Player:
def __init__(self):
starts = [1, 16, 31, 46, 61]
self.board = np.array([sample(range(i, i + 15), 5) for i in starts])
self.flipped = np.zeros((5, 5), dtype=bool)
self.flipped[2, 2] = True
def check(self, value):
self.flipped |= (self.board == value)
return any([
np.any(np.sum(self.flipped, axis=0) == 5),
np.any(np.sum(self.flipped, axis=1) == 5),
np.sum(np.diag(self.flipped)) == 5,
np.sum(np.diag(np.rot90(self.flipped))) == 5
])
results = []
for n_players in range(10, 200, 10):
for _ in range(20):
rounds = 0
winners = []
players = [Player() for _ in range(n_players)]
values = set(range(1, 76))
while not winners:
rounds += 1
value = choice(list(values))
values.remove(value)
for i, player in enumerate(players):
if player.check(value):
winners.append(str(i))
results.append({
'rounds': rounds,
'players': n_players,
'winners': ','.join(winners)
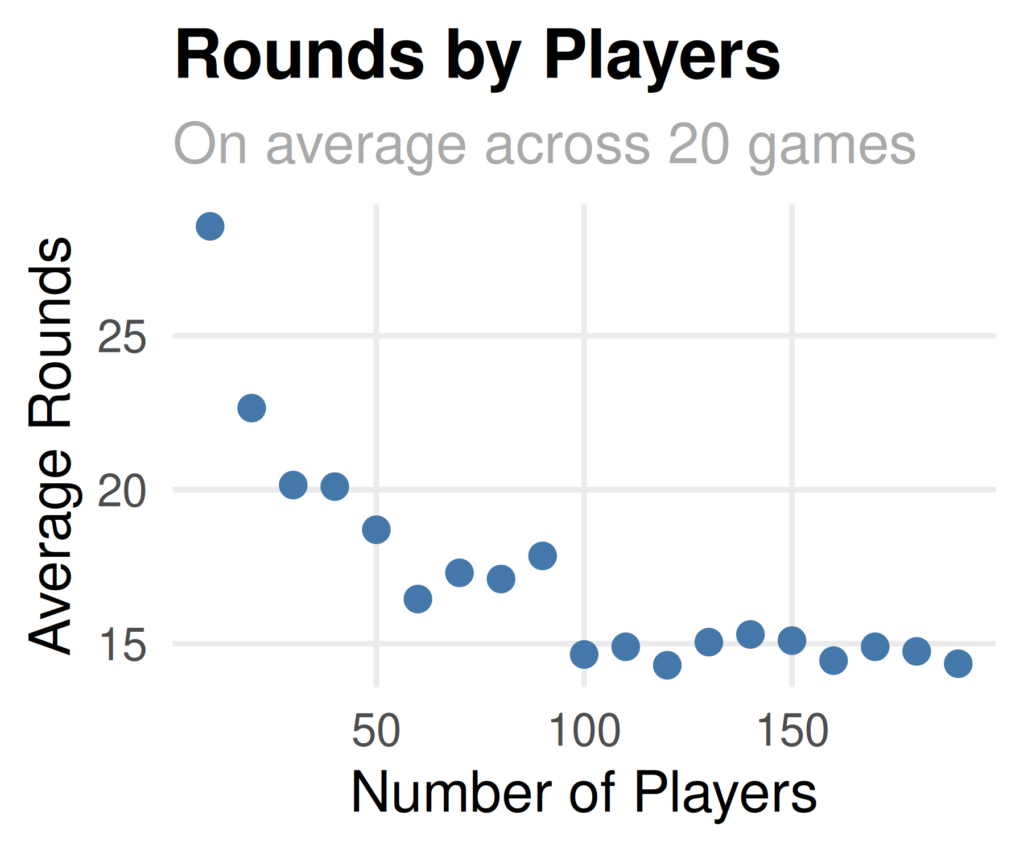
})First, I generated a plot that shows the number of rounds by number of players. As expected, this falls when the number of players increases!
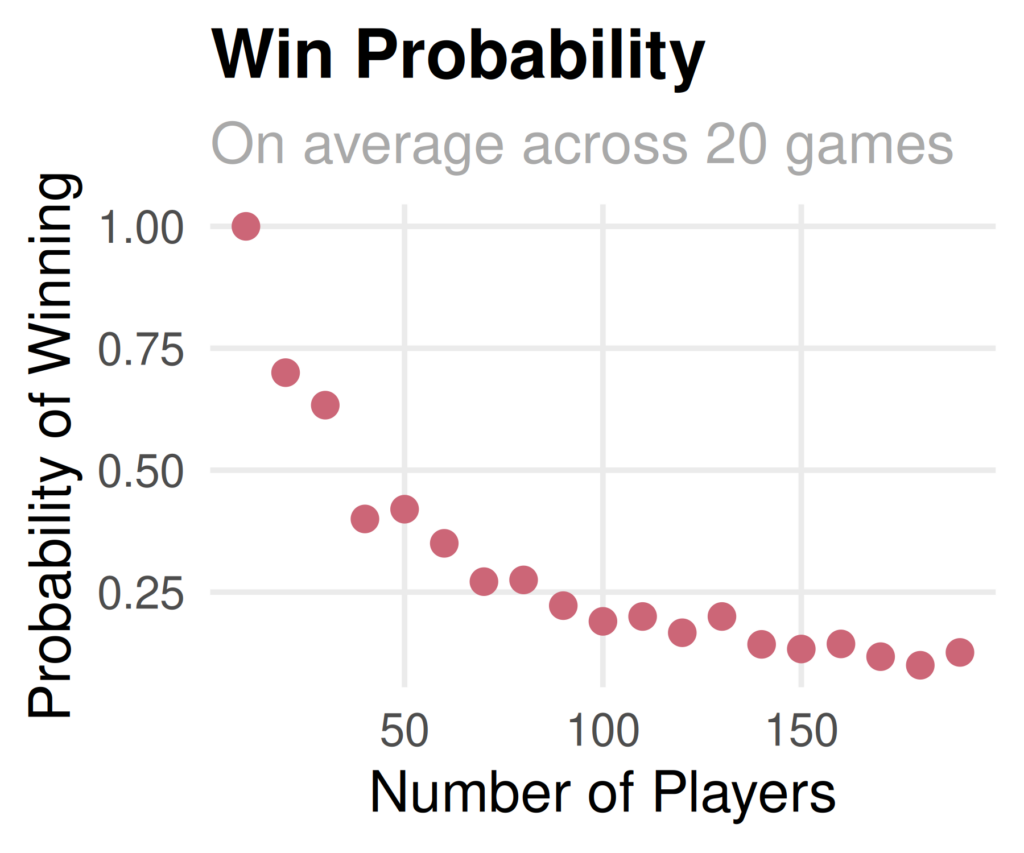
Finally, I looked at the probability of winning at least once by number of players. It appears that our simulated probability is 0.19 very similar to the computed probability of 0.182!